Finite size analogue of a heavy Fermi liquid in an atomic scale Kondo lattice

The scattering of conduction electrons in metals owing to impurities with magnetic moments is known as the Kondo effect, after Jun Kondo, who analyzed the phenomenon in 1964. This scattering increases the electrical resistance and has the consequence that, in contrast to ordinary metals, the resistance reaches a minimum as the temperature is lowered and then increases as the temperature is lowered further.

The Kondo effect is a collective one involving an indirect exchange interaction of the conduction electrons with a paramagnetic impurity. In paramagnetism, atoms or molecules have net orbital or spin magnetic moments. Actually, conduction electrons scattering off a magnetic impurity can screen the localized magnetic moment by forming a nonmagnetic many-particle singlet state, the Kondo many-body state (KS). In this way, the KS can be understood as the coupling of the quantum numbers of the conduction electrons and the localized moment to form a hybrid quasiparticle.

Figure 1. Schematic phase diagram of a Kondo lattice. The four possible phases of a Kondo lattice: a) Paramagnetic (PM) regime. b) Single-ion Kondo state (KS) with non-interacting impurities. c) Magnetically ordered state via RKKY interaction. d) Heavy Fermi liquid (HFL) phase. J is the exchange coupling between the local magnetic states (big arrows) and the Fermi gas (occupying the grey regions), and ρ the density of states of the conduction electron bath around the Fermi level.

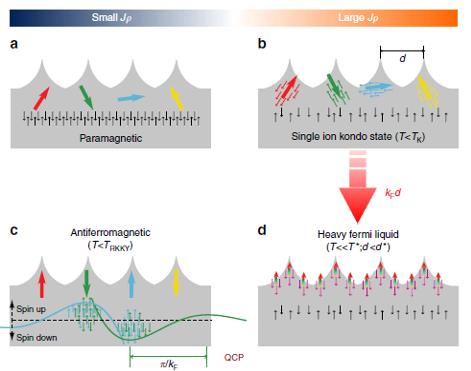
A Kondo lattice is a set of localized magnetic impurities arranged in a regular pattern, which interacts with a bath of delocalized conduction electrons. When the two subsystems are weakly coupled, the Kondo lattice falls in the paramagnetic or antiferromagnetic (AFM) regimes. In the limit of a large coupling strength between localized moments and extended states of the conduction electrons, the two subsystems cannot be treated separately. Thus, the Kondo lattice introduces a new energy scale, related to a temperature T*, which plays the role of Kondo temperature – the one limiting the validity of the Kondo results – in the sense that below T* the magnetic susceptibility starts being anomalously reduced due to partial screening. In an extended Kondo lattice, for temperatures well below T*, the system falls in the heavy Fermi liquid phase.

This term, heavy Fermi liquid (HFL), merits some clarification. Landau–Fermi liquid theory is a theoretical model of interacting fermions that describes the normal state of most metals at sufficiently low temperatures. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas (i.e. non-interacting fermions), and why other properties differ. Elements with 4f or 5f electrons in unfilled electron bands and their compounds , which have ions carrying magnetic moments but do not magnetically order, or only do so at very low temperatures, are generally known as heavy fermion or heavy electron systems because the scattering of the conduction electrons with the magnetic ions results in a strongly enhanced (renormalized) effective mass, as in the Kondo systems. The effective mass can be of the order 1000 times that of the real mass of the electrons. The low temperature behavior of many of these compounds can be understood in terms of a Fermi liquid of heavy quasiparticles, with induced narrow band-like states (renormalized bands) in the region of the Fermi level.

The HFL state is non-magnetic, because the conduction electrons fully screen the lattice spins. As in the case of the single-ion KS, the localized magnetic states contribute to the quasiparticle band developed by the coupled Kondo states. For this reason, this process is often called spin de-confinement.

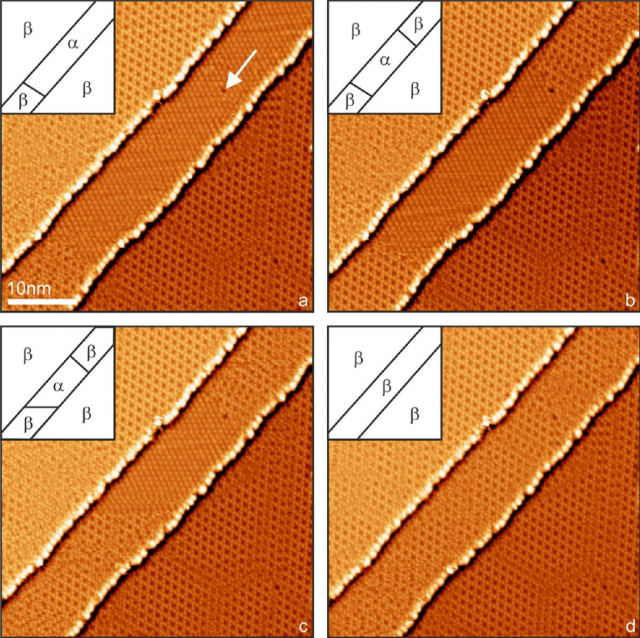
Now, a team of researchers, including Roberto Robles (CFM), Nicolás Lorente (CFM & DIPC) and Ikerbasque Research Professor José Ignacio Pascual (CIC nanoGUNE), has fabricated ¹ chains of coupled single-ion Kondo resonances by atomic manipulation in order to characterize in real space the crossover between the KS and the finite size analogue to a HFL.

Figure 2. Spin de-confinement in 1-D artificial Kondo lattices.

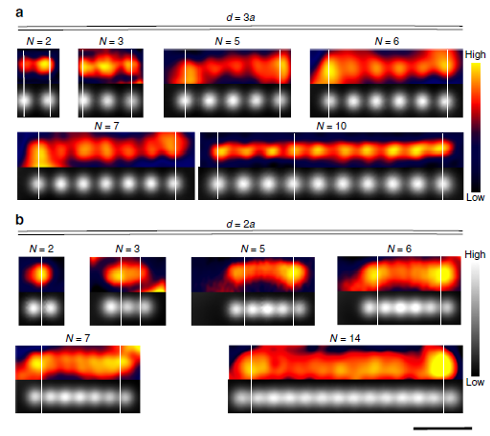
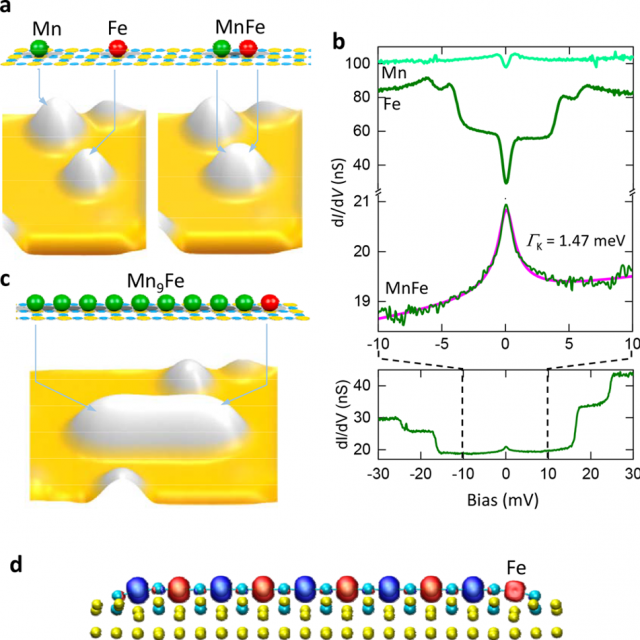
The researchers selected a sample with a strong coupling, so that Kondo screening overcomes any intersite interaction. The 3d orbitals of individual Co atoms adsorbed on a clean Ag(111) surface played the role of localized spins and metal host, respectively.

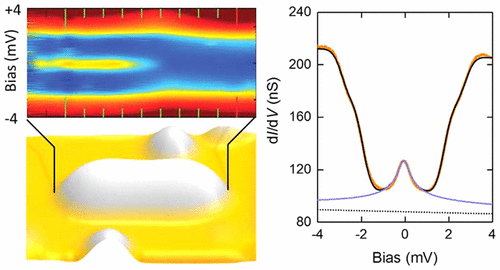
The onset of the surface conduction band of Ag(111) is right below the Fermi level, which gives rise to strong fluctuations of the density of screening electrons and an anomalously large Fermi wavelength. By means of an analysis of the multiimpurity Anderson model, the researchers linked the Ag(111) surface electronic structure to the experimental fingerprints of coherent and collective screening of the artificial Kondo lattice. They probed experimentally the de-confinement of Co magnetic moments upon formation of a collective KS by imaging the amplitude of the Kondo resonance in tunneling conductance spectra, which delocalizes away from the position of the impurity centres.

They were able to visualize in real space the onset of HFL behaviour as the redistribution of the Kondo amplitude (and consequently spin de-confinement). In dimers, it appeared as a delocalization of the Kondo amplitude towards its center. In chains, it manifested as patterns. The possibility of observing the real space structures in the adatom Kondo lattice is intimately linked to the fact that the chains are finite.

Apart from the Kondo temperature, the theoretical model developed reproduces the essential experimental observations without adjustable parameters: some are fixed by the experimental conditions, and the leading dimension of the electron gas is two. Therefore, this microscopic description should apply for different material parameters, and for arbitrary lattice site and dimensions, laying foundations to further investigations of correlated nanostructures engineered with atomic precision.

References

1. María Moro-Lagares, Richard Korytár, Marten Piantek, Roberto Robles, Nicolás Lorente, Jose I. Pascual, M. Ricardo Ibarra & David Serrate (2019) Real space manifestations of coherent screening in atomic scale Kondo lattices Nature Communications doi: 10.1038/s41467-019-10103-5 ↩

A Kondo effect by manipulating entangled spin chains

The scattering of conduction electrons in metals owing to impurities with magnetic moments is known as the Kondo effect, after Jun Kondo, who analysed the phenomenon in 1964. This scattering increases the electrical resistance and has the consequence that, in contrast to ordinary metals, the resistance reaches a minimum as the temperature is lowered and then increases as the temperature is lowered further.
The Kondo effect is a collective one involving an indirect exchange interaction of the conduction electrons with a paramagnetic impurity. In paramagnetism, atoms or molecules have net orbital or spin magnetic moments.
Actually, conduction electrons scattering off a magnetic impurity can screen the localized magnetic moment by forming a nonmagnetic many-particle singlet state. On a metallic surface, this Kondo screening manifests itself as a prominent zero-bias resonance in scanning tunneling microscope (STM) differential conductance measurements.
Still, a fully quantitative description of the Kondo effect is a very difficult many-body-problem. Even if ample experimental evidence exists for Kondo resonances of single spins on metals, either atomic or molecular, an entirely different world is revealed when several spins interact on metallic hosts. An extensive body of theoretical work explores the rich range of new states of matter that can be created from the competition of Kondo screening and interspin interactions. These phenomena exhibit extraordinary complexity but offer great potential if the emergent quantum states could be controlled.
The Kondo effect in spin-coupled chains has been proposed as a means of transmitting quantum coherent information in solid-state environments. This concept requires ways to extend and manipulate the Kondo effect on the atomic level. To date, in most scenarios considered experimentally, each spin is individually Kondo-screened, and the interaction among spins drives the preexisting Kondo effect into a new phase of matter.
But, what if we could create emergent Kondo states in nanostructure systems built from atoms that, individually, are not Kondo screened? Now a team of researchers, with the participation of Nicolás Lorente from CFM and DIPC, has created ¹ spin chains in which a strongly correlated Kondo state emerges from magnetic coupling of transition-metal atoms. The researchers built these linear chains – up to ten atoms in length – by placing iron (Fe) and manganese (Mn) atoms on a monolayer film of copper nitride (Cu₂N) with a STM.

Emergence of Kondo screening in MnxFe spin chains. (a) Ball model and STM images of the construction of a MnFe dimer by adding a Mn atom (green) to an Fe atom (red) on the Cu2N surface (Cu atoms yellow, N atoms blue). (b) Differential conductance spectra, dI/dV(V), for a Mn atom, a Fe atom, and a MnFe chain. (c) Ball model and STM image of Mn9Fe spin chain after it was constructed from MnFe in (a) by adding eight additional Mn atoms. (d) Spin density distribution on Mn9Fe chain calculated by density functional theory (see Methods) shown as the density difference between spin-up (blue) and spin-down (red) states.

They found that chains with one Fe and an odd number of Mn atoms exhibit a collective Kondo state. The emergent Kondo resonance is spatially distributed along the chain. Its strength can be controlled by mixing atoms of the metal elements and manipulating their spatial distribution.
The Kondo state in the composite system appears only if the spin−spin interactions within the chain are engineered to entangle all atomic spins with each other and form a doubly degenerate ground state that enables electrons from the host metal to flip all spins in the chain by a single electron scattering event.
The atomically precise construction allows the exact determination of the chain composition and the tuning of the coupling strengths. These determine the degree of interatomic entanglement which influences the probability of a spin-flip scattering and the resulting efficiency of the Kondo screening. In other words, the control the researchers achieve over the atomic entanglement in the chain means they control the emergence of a many-body electronic state.
The results demonstrate that it is experimentally feasible to create a Kondo ground state within a chain of atoms with large magnetic moments. The emergent Kondo state can be tuned by a competition between interatomic spin interaction and magneto-crystalline anisotropy of the constituent atoms.
The Kondo state, the researchers conclude, depends on the specific atomic composition of the spin chain and is characterized by the degree of entanglement among the atoms of the chain. This indicates that surface-adsorbed spin chains can serve as prototype systems for the exploration of correlated condensed-matter phases, where the electron correlations are tailored by the specific design of the atomic chains.
The method developed can in principle be generalized to a broader class of materials where electron−electron interaction can be tuned by structure and composition.

References

1. Deung-Jang Choi, Roberto Robles, Shichao Yan, Jacob A. J. Burgess, Steffen Rolf-Pissarczyk, Jean-Pierre Gauyacq, Nicolás Lorente, Markus Ternes, and Sebastian Loth (2017) Building Complex Kondo Impurities by Manipulating Entangled Spin Chains Nano Letters doi: 10.1021/acs.nanolett.7b02882 ↩

A 2D phase transition controlled by an electric field

Figure 1. STM image showing the coexistence of the α phase (lower left) and the β phase (upper right) separated by an atomic step of the copper substrate. The inset in the upper left corner shows the atomically resolved bare copper surface on the same lateral scale.

A phase may be defined as a homogeneous portion of a system that has uniform physical and chemical characteristics. Every pure material is considered to be a phase; so also is every solid, liquid, and gaseous solution. For example, a sugar–water syrup solution is one phase, and solid sugar is another. Each has different physical properties (one is a liquid, the other is a solid); furthermore, each is different chemically (i.e., has a different chemical composition); one is virtually pure sugar, the other is a solution of H₂O and C₁₂H₂₂O₁₁.
If more than one phase is present in a given system, each will have its own distinct properties, and a boundary separating the phases will exist across which there will be a discontinuous and abrupt change in physical and/or chemical characteristics. When two phases are present in a system, it is not necessary that there be a difference in both physical and chemical properties; a disparity in one or the other set of properties is sufficient. When water and ice are present in a container, two separate phases exist; they are physically dissimilar (one is a solid, the other is a liquid) but identical in chemical makeup.
Also, when a substance can exist in two or more polymorphic forms (different arrangements of the atoms, as in two different crystalline structures), each of these structures is a separate phase because their respective physical characteristics differ, and this difference can be measured in the form of a macroscopic variable, like conductivity or magnetization.
Phase transitions are ubiquitous in science, from fundamental physics, chemistry, or biology to ecological or even social systems. These transitions have a broad range of applications, from data storage to drug delivery. Phase transitions manifest themselves as changes, as we have noted, of a macroscopic physical characteristic.
For a detailed understanding of the different phases as well as the mechanism of phase transitions, knowledge about the individual objects is required. Various techniques based on microscopy or diffraction have been applied to analyse the structure of different phases.
The case of the arrangement of adsorbates on a surface is especially important in technological and fundamental research. It is is governed by interactions between the adsorbate and the atoms of the supporting surface as well as between the adsorbates themselves. The geometric structure these adsorbates assemble into can be studied by ensemble averaging techniques like electron diffraction or real space imaging techniques like low electron energy microscopy (LEEM), electron microscopy, scanning tunneling microscopy (STM), and atomic force microscopy (AFM).
These latter two techniques (STM and AFM) allow for the determination of the positions of individual atoms or molecules on the atomic scale. Not only that, the tip of an STM or AFM may act as a local probe to provide a stimulus to induce phase changes.
Now, Nicolás Lorente, from DIPC and ICM, and a team of researchers have used¹ the tip of an STM to induce a structural phase transition between two phases of a monolayer of CO on a Cu(111) surface (see Figure 1). The reversible transitions between phases are caused by the electric field between the tip and the sample surface.
The experiments reveal a structural 2D phase transition between two rather complex molecular arrangements of CO on Cu(111), which is reversible despite the slightly different coverages. Because the transition is efficiently triggered by the electric field of an STM tip using voltages in the range of ±3 V, it opens a new field of research, especially due to the excellent control of the experimental conditions.

Figure 2. Expansion of the β phase. Prior to the measurements, a small area was transformed to the α phase by sweeping the bias voltage to −1.5 V. The sequence of STM images (a−d) reveals how the α phase is successively converted back to the β phase

In contrast to thermally induced transitions, the researchers found that very localized areas can be reversibly transformed and patterns of the two phases may be written on a small scale (see Figure 2) and that the switching times can be very fast.
It is remarkable that, in contrast to the common observation of phase transitions, not only macroscopic quantities of a large ensemble may be studied but also the position of every element of the system can be directly accessed. Given the ease of the experiment, it is an ideal model system to be used to better understand the physics of structural phase transitions on the atomic scale.

References

1. B. Wortmann , D. van Vörden, P. Graf, R. Robles, P. Abufager, N. Lorente, C. A. Bobisch, and R. Möller (2016) Reversible 2D Phase Transition Driven By an Electric Field: Visualization and Control on the Atomic Scale Nano Letters DOI: 10.1021/acs.nanolett.5b04174 ↩